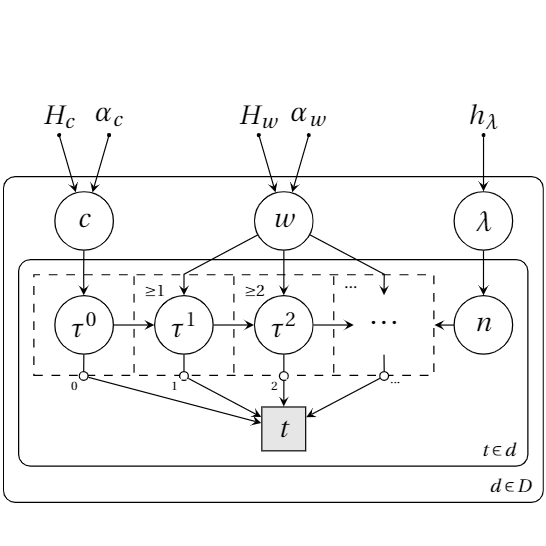
Abstract
Pitch-class distributions are of central relevance in music information retrieval, computational musicology and various other fields, such as music perception and cognition. However, despite their structure being closely related to the cognitively and musically relevant properties of a piece, many existing approaches treat pitch-class distributions as fixed templates. In this paper, we introduce the Tonal Diffusion Model, which provides a more structured and interpretable statistical model of pitch-class distributions by incorporating geometric and algebraic structures known from music theory as well as insights from music cognition. Our model explains the pitch-class distributions of musical pieces by assuming tones to be generated through a latent cognitive process on the Tonnetz, a well-established representation for harmonic relations. Specifically, we assume that all tones in a piece are generated by taking a sequence of interval steps on the Tonnetz starting from a unique tonal origin. We provide a description in terms of a Bayesian generative model and show how the latent variables and parameters can be efficiently inferred. The model is quantitatively evaluated on a corpus of 248 pieces from the Baroque, Classical, and Romantic era and describes the empirical pitch-class distributions more accurately than conventional template-based models. On three concrete musical examples, we demonstrate that our model captures relevant harmonic characteristics of the pieces in a compact and interpretable way, also reflecting stylistic aspects of the respective epoch.
Fabian C. Moss
Assistant Professor for Digital Music Philology and Music Theory
Fabian C. Moss is an assistant professor for Digital Music Philology and Music Theory at Julius-Maximilians University Würzburg (JMU), Germany.