Wavescapes: A visual hierarchical analysis of tonality using the discrete Fourier transform
Abstract
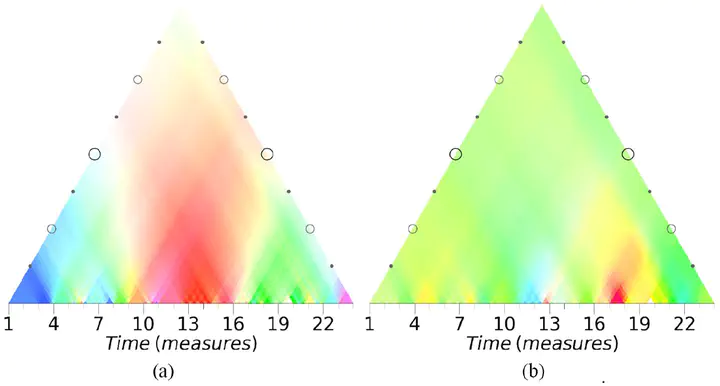
Many structural aspects of music, such as tonality, can be expressed using hierarchical representations. In music analysis, so-called keyscapes can be used to map a key estimate (e.g., C major, F minor) to each subsection of a piece of music, thus providing an intuitive visual representation of its tonality, in particular of the hierarchical organization of local and global keys. However, that approach is limited in that the mapping relies on assumptions that are specific to common-practice tonality, such as the existence of 24 major and minor keys. This limitation can be circumvented by applying the discrete Fourier transform (DFT) to the tonal space. The DFT does not rely on style-specific theoretical assumptions but only presupposes an encoding of the music as pitch classes in 12-tone equal temperament. We introduce wavescapes, a novel visualization method for tonal hierarchies that combines the visual representation of keyscapes with music analysis based on the DFT. Since wavescapes produce visual analyses deterministically, a number of potential subjective biases are removed. By concentrating on one or more Fourier coefficients, the role of the analyst is thus focused on the interpretation and contextualization of the results. We illustrate the usefulness of this method for computational music theory by analyzing eight compositions from different historical epochs and composers (Josquin, Bach, Liszt, Chopin, Scriabin, Webern, Coltrane, Ligeti) in terms of the phase and magnitude of several Fourier coefficients. We also provide a Python library that allows such visualizations to be easily generated for any piece of music for which a symbolic score or audio recording is available.