Abstract
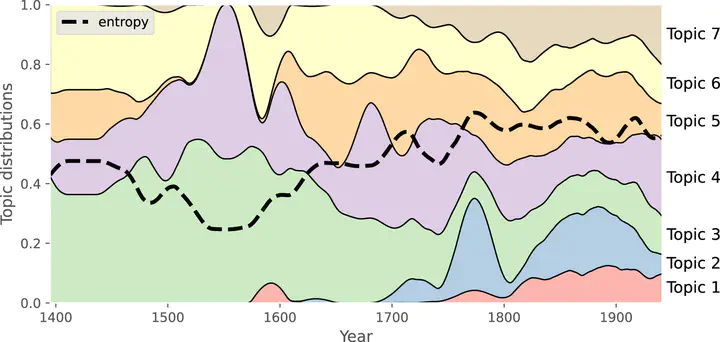
Music analysis, in particular harmonic analysis, is concerned with the way pitches are organized in pieces of music, and a range of empirical applications have been developed, for example, for chord recognition or key finding. Naturally, these approaches rely on some operationalization of the concepts they aim to investigate. In this study, we take a complementary approach and discover latent tonal structures in an unsupervised manner. We use the topic model Latent Dirichlet Allocation and apply it to a large historical corpus of musical pieces from the Western classical tradition. This method conceives topics as distributions of pitch classes without assuming a priori that they correspond to either chords, keys, or other harmonic phenomena. To illustrate the generative process assumed by the model, we create an artificial corpus with arbitrary parameter settings and compare the sampled pieces to real compositions. The results we obtain by applying the topic model to the musical corpus show that the inferred topics have music-theoretically meaningful interpretations. In particular, topics cover contiguous segments on the line of fifths and mostly correspond to diatonic sets. Moreover, tracing the prominence of topics over the course of music history over ∼600 years reflects changes in the ways pitch classes are employed in musical compositions and reveals particularly strong changes at the transition from common-practice to extended tonality in the 19th century.
Fabian C. Moss
Assistant Professor for Digital Music Philology and Music Theory
Fabian C. Moss is an assistant professor for Digital Music Philology and Music Theory at Julius-Maximilians University Würzburg (JMU), Germany.