Abstract
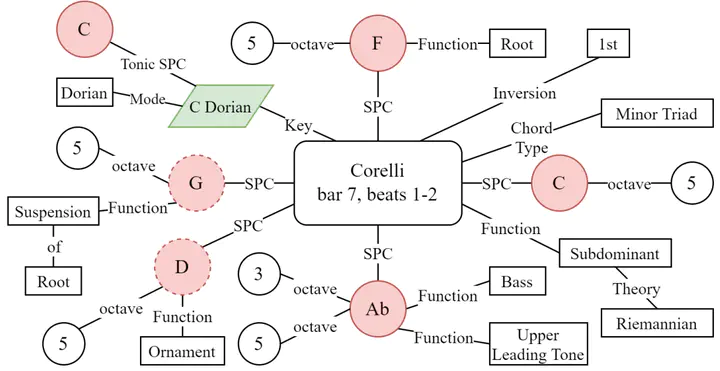
Chord-based harmony is an important aspect of many types of Western music, across genres, regions, and historical eras. However, the consistent representation and comparison of harmony across a wide range of styles (e.g. classical music, Jazz, Rock, or Pop) is a challenging task. Moreover, even within a single musical style, multiple theories of harmony may exist, each relying on its own (possibly implicit) assumptions and leading to harmonic analyses with a distinct focus (e.g. on the root of a chord vs. its bass note) or representation (e.g. spelled vs. enharmonic pitch classes). Cross-stylistic comparisons (as well as comparisons within a single style involving multiple annotation systems) are therefore even more difficult, particularly in a large-scale computational setting that requires a common overarching representation. To address these problems, we propose a model which allows for the representation of chords at multiple levels of abstraction: from chord realizations on the score level (if available), to pitch-class collections (including a potential application of different equivalences, such as enharmonic or octave equivalence), to pitch- and chord-level functions and higher-order abstractions. Importantly, our proposed model is also well-defined for theories which do not specify information at each level of abstraction (e.g., some theories make no claims about harmonic function), representing only those harmonic properties that are included and inducing others where possible (e.g., deriving scale degrees from root and key information). Our model thus represents an important step towards a unified representation of harmony and its various applications.
Fabian C. Moss
Assistant Professor for Digital Music Philology and Music Theory
Fabian C. Moss is an assistant professor for Digital Music Philology and Music Theory at Julius-Maximilians University Würzburg (JMU), Germany.