Fabian C. Moss

Digital Music Philology and Music Theory

Julius-Maximilians-Universität Würzburg

Welcome!

I am a tenure-track assistant professor for Digital Music Philology and Music Theory in the Institut für Musikforschung at Julius-Maximilians University Würzburg (JMU), Germany, part of the extended collegial board of the Zentrum für Philologie und Digitalität (ZPD), and member of the Graduate School Humanities (GSH).

In my research, I bridge concepts and methodologies from the humanities and the sciences, and aim to understand music and its structure from an inherently interdisciplinary perspective, involving fields such as musicology and music theory, mathematics, music information retrieval, data science and machine learning, music cognition, and the digital humanities. One of my central interests lies in analysing large digital corpora in order to better understand musical styles, especially from a historical viewpoint. More specifically, I work with large symbolic datasets of musical scores and harmonic annotations. I am also interested in computational modeling of music and its perception, and am fascinated by quantitative approaches to model historical processes.

I teach courses covering a wide range of topics in music theory, computational musicology, and digital tools, and provide professional service as an advisory board member for Computational Humanities Research and Analitica - Revista Online di Studi Musicali as well as reviewing service for several conferences and journals (see CV).

Before my appointment to JMU, I have worked as a Research Fellow in Cultural Analytics at University of Amsterdam (Media Studies Department & Data Science Centre), and before that as doctoral and postdoctoral researcher at École Polytechnique Fédérale de Lausanne (EPFL)’s Digital and Cognitive Musicology Lab. Supported by the German Academic Exchange Service (DAAD), I visited the Department of Linguistics and Philosophy at the Massachusetts Institute of Technology (MIT) as a research PhD student and spent a semester at Escola Superior de Música de Catalunya (ESMUC) funded by the ERASMUS program of the European Union.

Research Interests

Computational Musicology · Corpus Studies · Music Theory & Analysis · Digital Humanities · Artificial Intelligence · Cultural Evolution

Videos

Research & Projects

Present and past

Fabian C. Moss

Jan 1, 2025 digital humanities, music theory

DigiMusTh

The DigitMusTh project focuses on the digital collection and analysis of historical music theory texts, with a particular emphasis on the 19th-century debate on major-minor dualism. While large digital collections of music theory texts already exist in other languages there is currently no comparable collection for German-language texts, despite their central role in European music theory since the 18th century. DigitMusTh aims to fill this gap by creating a sustainable and expandable digital edition that offers new perspectives for both musicology and the digital humanities.

Fabian C. Moss

Jan 4, 2024 digital humanities, music theory

Digital Choro

The project “Digtial Choro: Exploring the potential of digitization and computational models for Brazil’s musical cultural heritage” aims to utilize digitization and data-driven methods to develop computational models of the complex genesis of Choro, a Brazilian instrumental music genre.

Fabian C. Moss

Jul 4, 2023

Computational and Digital Approaches to Music Scholarship (CODAMUS)

As musicologists continue to explore new ways of analyzing, understanding, and creating music through the use of digital methods and computational models, new questions and avenues for research and scholarship arise. CODAMUS aims at providing a glimpse into the exciting intersections of music and technology.

Fabian C. Moss

Jul 4, 2023 digital humanities, music theory

Virtual Tonal Spaces (VTS)

The high dimensionality of music means that even digital representations on screen do not convey tonal spaces with sufficient clarity. Here, the extended field of view and the higher degrees of freedom of virtual reality environments offer the possibility to express musical parameters more clearly through aesthetic parameters and thus generate a better understanding among learners.

Fabian C. Moss, Johannes Hentschel, Markus Neuwirth, Martin Rohrmeier

Sep 13, 2022

Representing Harmony

Harmony is an essential component of Western music at least since the middle ages up to the present day. In recent decades, musicologists have engaged more and more with computational methods and created machine-readable datasets in order to study harmony on a larger scale.

Fabian C. Moss, Daniel Harasim, Giovanni Affatato

Jul 1, 2021 music theory, digital humanities

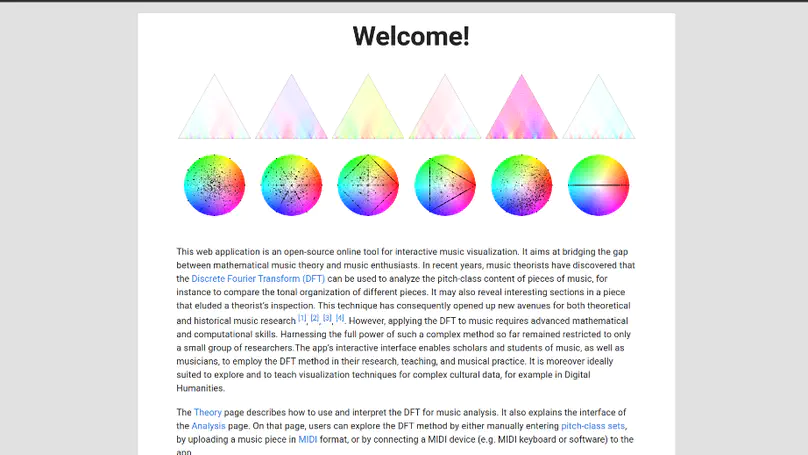
Enabling interactive music visualization for a wider community (midiVERTO)

This project aims at bridging the gap between mathematical music theory and music enthusiasts. In recent years, music theorists have discovered that the Discrete Fourier Transform (DFT) can be used to analyze the pitch-class content of pieces of music, for instance to compare the tonal organization of different pieces.

Fabian C. Moss, François Bavaud, Colline Métrailler, Maik Köster, Melinda Femminis

Jan 1, 2021 digital humanities, music theory, corpus studies

Digitizing the Dualism Debate (DDD)

The “dualism debate”, a ‘hot topic’ in 19th-century German music theory, is concerned with the mutual relationship of major and minor triads, specifically whether the minor triad is a mere derivative of the major triad or whether it can be derived from first principles on its own right. This project strives to reconstruct and critically evaluate the discursive relations within this debate by using the combined power of qualitative-historical and quantitative-numerical methods and thus serve to build methodological bridges between the humanities and the sciences.